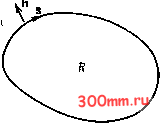3) смешанное условие, если условие Робина, например duldn + ku=f, k> О на OR.

При формулировке вспомогательных условий (2) и (3) символ д/дп обозначает производную по внешней нормали.

При рассмотрении большинства течений, требующих для своего анализа решения уравнений Навье - Стокса в примитивных переменных (и, v, р и т. д.), по меньшей мере одна составляющая скорости задается на границе втекания. Это дает граничное условие Дирихле для скорости. По отношению к уравнению для потенциала скоростей, определяющему течение невязкой сжимаемой жидкости, условие дф/ди = = О на поверхности тела является условием Неймана. Смешанные условия редко встречаются в гидро-Рис. 2.2. Вычислительная об- аэродинамике, однако встречаются ласть R. в теории конвективной теплопере-

дачи. С вычислительной точки зрения вспомогательные условия Дирихле могут быть поставлены точно, если только функция / является аналитической. Однако при постановке условий Неймана или сломанных условий вносятся ошибки (см. § 7.3).

2.1.3. Классификация с помоиью характеристик

По отношению к дифференциальным уравнениям в частных производных с двумя независимыми переменными классификация, т. е. отнесение к эллиптическому, параболическому или гиперболическому типу, может быть осуществлена за счет предварительного отыскания характеристических направлений, только вдоль которых определяющие уравнения позволяют находить полные дифференциалы.

Для одного ДУЧП первого порядка с двумя независимыми переменными

в каждой точке существует единственная вещественная характеристика, причем характеристическое направление определяется соотношением (см. рис. 2.5)

Вдоль характеристического направления уравнение (2.5) приводит к соотношениям

du С du С тч

-rfr = T ж-в- М

Уравнение (2.5) является гиперболическим ДУЧП, и соотношения (2.7) могут быть проинтегрированы как обыкновенные дифференциальные уравнения вдоль линий сетки, определяемой соотношениями (2.6), если только начальные данные заданы на линии, не являющейся характеристикой.

То же самое представление о характеристических направлениях может быть использовано и в связи с изучением ДУЧП второго порядка с двумя независимыми переменными, такого как (2.1). Так как из условий (2.2) следует, что тип ДУЧП определяется лишь коэффициентами при высших производных, то уравнение (2.1) удобно записать в виде

где Н включает в себя все члены с первыми производными и без производных из уравнения (2.1), а коэффициенты Л, В и С могут быть функциями X и у. Для каждой точки области можно построить два направления, вдоль которых интегрирование уравнения (2.8) связано только с полными дифференциалами. Существование этих (характеристических) направлений имеет непосредственную связь с классификацией ДУЧП.

Для простоты представления введем следующие обозначения:

-дх* -ду* дх -di

Внутри рассматриваемой области располагается кривая /С, на которой Р, Q, R, Т и и удовлетворяют уравнению (2.8). По направлению касательной к К дифференциалы Р и Q удовлетворяют соотношениям

dP = Rdx + Sdy, (2.10)

dQ = Sdx + Tdy, (2.11)

а уравнение (2.8) может быть записано как

AR + BS + CT + fI = 0. (2.12)

В соотношениях (2.10) и (2.11) величина dy/dx определяет угол наклона касательной к К. Используя (2.10) и (2.11), из

40 Гл. 2. Дифференциальные уравнения в частных производных уравнения (2.12) можно исключить R и Т; тогда получим

= 0. (2.13)

Если выбрать dy/dx таким образом, что

Ш- Ш+С = 0, (2.14>

ТО уравнение (2.13) приводится к более простому соотношению, связывающему dP/dx и dQ/dx, а именно

Два решения уравнения (2.14) определяют два характеристических направления, на которых выполняется соотношение (2.15). Если сравнить (2.14) с (2.2), то ясно, что уравнение (2.8) является

1) гиперболическим ДУЧП, если существуют две вещественные характеристики,

2) параболическим ДУЧП, если существует одна вещественная характеристика,

3) эллиптическим ДУЧП, если характеристики комплексны.

Таким образом, дискриминант - 4АС определяет не только-тип ДУЧП, но и свойства характеристик.

Пока что исследование типа ДУЧП проводилось с использованием декартовых координат. Возникает важный вопрос - может ли преобразование координат такого рода, какой будет описан в гл. 12, изменить тип дифференциального уравнения в частных производных?

Таким образом, вместо (л:, у) вводятся новые независимые переменные (g, т]), причем предполагается, что преобразования g = g(jc, у) и ц=ц(х, у) известны. Производные преобразуются по формулам типа (см. § 12.1)

ди ди . ди ,

= 1х+Цх, (2.16)

где 1л; = дЦдх и т. д. После некоторых манипуляций уравнение (2.8) приводится к виду

В = 2А1,У], + В Ц.Цу + 1,ц,) + 2ауГ]у, (2.18)