ритма и его согласованность с первоначальным дифференциальным уравнением в частных производных, тогда как обычно очень трудно установить сходимость получаемого приближенного решения к решению упомянутого дифференциального уравнения.

Большинство реальных задач гидроаэродинамики нелинейны и представляют собой краевые задачи или же смешанные задачи с граничными и начальными условиями, так что теорема Лакса об эквивалентности не всегда строго применима. Исходя из этого следует интерпретировать теорему Лакса об эквивалентности как обеспечивающую необходимые, но не всегда достаточные условия. Уравнение эквивалентности Лакса, представленное в форме (4.1), полезно для целей исключения несогласованных дискретизаций и неустойчивых алгоритмов.

4J.2. Численная сходимость

Применительно к тем уравнениям, которым подчиняется течение жидкости и газа, обычно невозможно теоретически продемонстрировать сходимость. Однако для задач, обладающих точными решениями, таких, как задачи, связанные с уравнением диффузии, можно получить серию численных решений на последовательно измельчаемых сетках и рассчитать ошибку решения. Сходимость означает, что ошибка решения должна уменьшаться до нуля по мере того, как размеры элементов сетки приближаются к нулю.

Решения, полученные для программы DIFF (см. рис. 3.13), были построены на последовательно измельчаемых пространственных сетках при Дх = 0.2, 0.1, 0.05 и 0.025. Соответствующие среднеквадратичные ошибки приведены в табл. 4.1 для .S = 0.50 и 0.30. Как видно из таблицы, среднеквадратичная ошибка уменьшается примерно пропорционально Ах. Основываясь на этих результатах, можно сделать вполне оправданный вывод о том, что измельчение сетки должно приводить к дальнейшему уменьшению среднеквадратичной ошибки и в

Таблица 4.1. Уменьшение среднеквадратичной ошибки решения при измельчении сетки

Ц (Ах)

-Z.0 -1.8 -1.6 -1.4 -1.2

i-1- -1-1-1-1-1 l

пределе при Дл: (при фиксированном 5), стремящемся к нулю решение алгебраических уравнений должно сходиться к точному решению.

Установление численной сходимости является довольно дорогостоящим процессом, так как при этом обычно необходима использовать очень мелкие сетки. Учитывая, что в вышеупомянутом примере величина 5 сохраняется постоянной, при каждом уменьшении Дл: вдвое шаг по времени уменьшается в четыре раза. Ошибка решения, приводимая в табл. 4.1, рассчитывается при / = 5000 с. Отсюда-следует, что при 5 = 0.30 решение на самой мелкой сетке требует 266 шагов по времени прежде чем будет рассчитана ошибка решения. Для уравнения диффузии g ш (3.1) с нулевыми граничными значениями и начальным значением Г(а:,0)= sin ял:, О х 1,. среднеквадратичная ошибка решения erms изображается гра-Ю фически на рис. 4.2 как функция Рис. 4.2. Численная сходимость размера ячейки Дл:. Повышенная для метода ВВЦП. степень сходимости (сходимость

четвертого порядка) выявляется очень четко при 5=1/6 в сравнении с другими значениями S 1/2 (сходимость второго порядка), т. е. степень сходимости пропорциональна Дл: при 5 = 1/6 и пропорциональна Дх2 в остальных случаях. Как это будет показано в § 4.2,. улучшенная степень сходимости при 5= 1/6 должна ожидаться на основании вида главного члена в выражении ошибки аппроксимации. Как правило, при достаточно малых размерах ячеек Дл: и At ошибка решения будет уменьшаться подобно ошибке аппроксимации при Ax-Q, At-Q.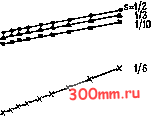

§ 4.2. Согласованность

Говорят, что система алгебраических уравнений, получен-. пая в результате процесса дискретизации, согласуется с первоначальным дифференциальным уравнением в частных производных, если в пределе, когда размеры ячеек сетки стремятся к нулю, система алгебраических уравнений эквивалентна дифференциальному уравнению в частных производных в каждой из узловых точек сетки.

Ясно, что наличие согласованности необходимо, если приближенное решение должно сойтись к решению рассматриваемого нами дифференциального уравнения в частных производных. Однако это условие не является достаточным, так как даже если система алгебраических уравнений окажется эквивалентной дифференциальному уравнению в частных производных при стремлении к нулю размеров ячеек, отсюда не следует, что решение данной системы алгебраических уравнений будет стремиться к решению исходного дифференциального уравнения. Например, если в программе DIFF задать 5 > 1/2, то решение, использующее алгоритм ВВЦП по формуле (3.41), будет быстро расходиться.

Техника проверки на согласованность требует, чтобы точное решение было подставлено в полученные после дискретизации алгебраические уравнения с последующим разложением всех узловых значений в ряды Тейлора в окрестности единственной точки. Для наличия согласованности полученное выражение должно состоять из первоначального дифференциального уравнения в частных производных, сложенного с остаточным членом. Структура остаточного члена должна быть такой, чтобы он обращался в нуль при измельчении сетки.

В данном параграфе мы проанализируем схему ВВЦП (п. 4.2.1) и чисто неявную схему (п. 4.2.2) с тем, чтобы проверить, представляют ли они согласованные дискретизации уравнения диффузии (3.1).

4.2.1. Схема ВВЦП

Схема ВВЦП (3.41) использовалась нами в п. 3.5.2 для получения решения одномерного уравнения диффузии. Подстановка величины Г/, представляющей точное решение уравнения диффузии в (/, п)-м узле, в приближенное выражение дает

Ti - = sfl-x + (1 - 25) + sfUu (4.3)

Нам необходимо определить, насколько близким является соответствие соотношения (4.3) уравнению диффузии (3.1) в (/, п)-м узле. Если каждый член соотношения (4.3) заменить разложениями в ряд Тейлора, построенными в (/, п)-и узле, то после некоторых упрощений получим

дТ f Г дТ

/ L дх

+ Е1 = 0, (4.4)

Е1 = 0.5 [Щ - а {) Щ + О {t А/). (4.5)