зволяет получить следующую систему уравнений, заменяющую (5.17):

г 1/3 1/4 1/5 -irai-j г1/2-

1/4 8/15 2/3 Яг = 2/3 . (5.20)

. 1/5 2/3 33/35 JLasJ 1з/4.

Применение метода подобластей с интервалами от О до 1/3, от 1/3 до 2/3 и от 2/3 до 1.0 приводит к следующей системе уравнений:

г 5/18 8/81 11/324 1 г а, 1 г 1/3-

3/18 20/81 69/324 = 1/3 (5.21)

. 1/18 26/81 163/324 JLoaJ L 1/3 .

Применение метода коллокации при оценке невязки в точках JC = О, 0.5 и 1.0 дает следующую систему уравнений:

Значения ai, 2 и з, полученные с помощью решения различными методами, приводятся в табл. 5.2, а соответствующие им приближенные решения (5.12)- в табл. 5.3.

Таблица 5.2. Сравнение коэффициентов в приближенных решениях уравнения dyldx - (/ = О

Оптимальное в смысле среднеквадратичной величины решение получается за счет минимизации среднеквадратичной ошибки с тремя неизвестными коэффициентами. Сравнение

различных решений по методам взвешенных невязок целесообразно проводить именно с таким, а не с точным решением. Ясно, что методы Галёркина, наименьших квадратов и подобластей приводят к решениям, близким к оптимальным.

Точность метода коллокаций весьма чувствительна к выбору контрольных точек. Если оценивать невязку при л: = 0.1127, 0.50 и 0.8873, то получается решение, идентичное решению по методу Галёркина.

Таблица 5.3, Сравнение приближенных решений уравнения dyldx - у = 0

Решения, приводимые в табл. 5.3, изображаются графически на рис. 5.2, и из графика ясно, что методы взвешенных невязок (за исключением, может быть, метода коллокаций) весьма эффективно реализуют минимизацию ошибки решения по всей области. В противоположность этому, метод разложения в ряд Тейлора, обеспечивающий совпадение с точным решением при X = 0.0, приводит к большой ошибке решения вдали от нулевой точки.

Различные методы взвешенных невязок подвергаются всестороннему сравнению в книге [Fletcher, 1984], где автор делает следующий вывод: Метод Галёркина дает результаты неизменно высокой степени точности, имея при этом столь же широкий диапазон приложений, как и любой другой метод

взвешенных невязок . В данной ситуации ценность метода Галёркина обусловливается тем, что он непосредственно приво-

0.002

Метод подобластей

-0.002

-0.004

-0,006-

Решение ; оптимальным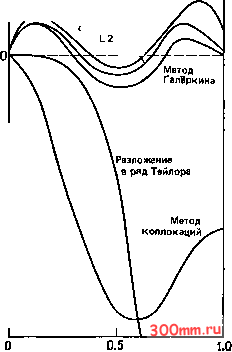

Рис. 5.2. Распределение ошибок для решений уравнения dy/dx - г/ = О, построенных методами взвешенных невязок (ЛГ = 3).

дит к методу Галёркина с конечными элементами, а также к спектральному методу Галёркина.

§ 5.2. Метод конечных объемов

Вышеназванный метод подобен методу подобластей, если не считать того, что здесь не вводится в явной форме какое-либо приближенное решение наподобие выражения (5.2). Этот метод оказывается особенно компактным, если определяющие уравнения включают только первые производные (см. п. 5.2.1). Если же присутствуют и вторые производные (см. п. 5.2.2), то требуются некоторые дополнительные операции.

10 к. Флетчер, т. 1